
질문
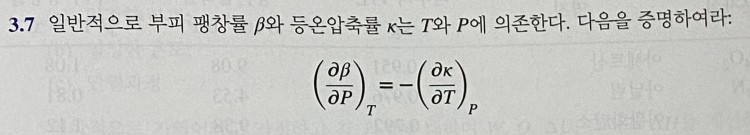
kin.naver.com/qna/detail.nhn?d1Id=11&dirId=1114&docId=370539865
열역학 부피팽창률 등온압축률 질문
이거 어떻게 푸나요ㅜㅜ
kin.naver.com
풀이
\[dv=\left ( \frac{\partial v}{dP} \right )_{T}dP+\left ( \frac{\partial v}{dT} \right )_{P}dT\]
\[\frac{dv}{v}=\frac{1}{v}\left ( \frac{\partial v}{dP} \right )_{T}dP+\frac{1}{v}\left ( \frac{\partial v}{dT} \right )_{P}dT\]
\[\frac{dv}{v}=d\left ( ln \left ( v\right ) \right )\]
\[\frac{1}{v}\left ( \frac{\partial v}{dP} \right )_{T}dP+\frac{1}{v}\left ( \frac{\partial v}{dT} \right )_{P}dT=-\kappa dP+\beta dT\]
압축계수 팽창계수 compressibility & expansion coefficient
압축계수 팽창계수 compressibility & expansion coefficient 체팽창계수 thermal expansion coefficient 등온압축계수 isothermal compressibility 등엔트로피압축계수 Isentropic compressibility 압..
syssurr.tistory.com
\[d\left ( ln \left ( v\right ) \right )=-\kappa dP+\beta dT\]
\[d\left ( ln \left ( v\right ) \right )\] 는 완전미분이므로
[열역학 Thermodynamics/12. 일반관계식 Thermodynamic Relations ] - 편미분 관계식 partial differential relations
편미분 관계식 partial differential relations
편미분 관계식 partial differential relations 열역학에서 z의 전미분이 exact이면 상태량(property) 이고 변화량은 으로 표기한다 inexact이면 경로함수(path function) 이고 변화량은으로 표기한다. [1]..
syssurr.tistory.com
\[-\left ( \frac{ \partial \kappa }{\partial T} \right )_{P}=\left ( \frac{ \partial \beta }{\partial P} \right )_{T}\]
'열역학 Thermodynamics > 문제와 풀이 Problems and Solutions' 카테고리의 다른 글
| 정압과정에서 내부에너지 감소? (0) | 2020.10.21 |
|---|---|
| 이상기체의 정적비열과 정압비열 관계 (0) | 2020.10.20 |
| 열역학 맥스웰 관계식 문제 증명 (편미분 방정식) (1) | 2020.06.17 |
| 열역학 제1법칙과 뉴턴의 운동 제2운동법칙 Newton's second law is a special case of the first law of thermodynamics (0) | 2020.06.04 |
| 밀폐계 정압과정의 열과 엔탈피 개념 문제 풀이 (0) | 2019.03.31 |
