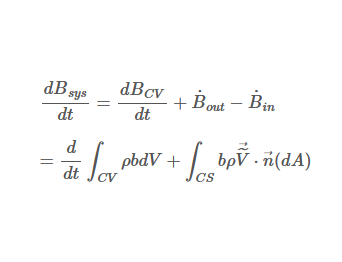
레이놀즈 수송정리 Reynolds Transport Theorem (RTT)

 

 

레이놀즈 수송정리 Reynolds Transport Theorem (RTT)

[1][2]

 

B를 질량, 에너지, 모멘텀과 같은 종량적 상태량 extensive property라고 하고

b를 b=B/m 으로 B의 강성적 상태량 intensive property라고 하자.

 

 

fixed control volume에서 시간 t에서 t+Δt에 따른 control volume이

아래 그림과 같이 변한다고 가정

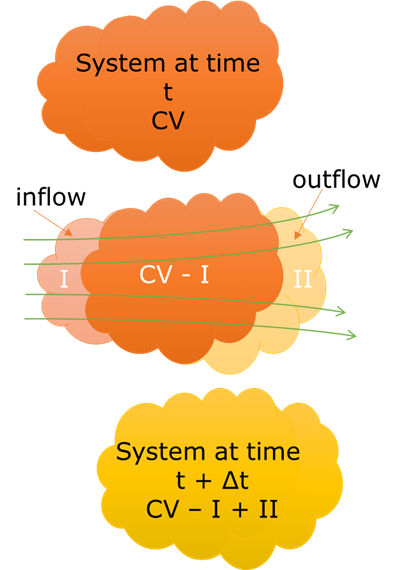
시간 t에서 CV를 system이라고 하면

$$B_{sys}(t)=B_{CV}(t)$$

 

시간 t+Δt에서CV - I + II을 system이라고 하면

$$B_{sys}(t+\mathrm{\Delta }t)=B_{CV}(t+\mathrm{\Delta }t)-B_I(t+\mathrm{\Delta }t)+B_{II}(t+\mathrm{\Delta }t)$$

 

시간 t+Δt와 t의 차이인 Δt 에 대한

$$B_{sys}(t+\mathrm{\Delta }t)-B_{sys}(t)$$

의 변화량은

 

$$\frac{B_{sys}(t+\mathrm{\Delta }t)-B_{sys}(t)}{(t+\mathrm{\Delta }t)-t}$$

Δt->0 일 때 위 식의 limit 값은

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_{sys}(t+\mathrm{\Delta }t)-B_{sys}(t)}{(t+\mathrm{\Delta }t)-t}$$

$$=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{\{B_{CV}(t+\mathrm{\Delta }t)-B_I(t+\mathrm{\Delta }t)+B_{II}(t+\mathrm{\Delta }t)\}-B_{CV}(t)}{(t+\mathrm{\Delta }t)-t}$$

$$=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{\{B_{CV}(t+\mathrm{\Delta }t)-B_{CV}(t)\}+B_{II}(t+\mathrm{\Delta }t)-B_I(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

 

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_{sys}(t+\mathrm{\Delta }t)-B_{sys}(t)}{(t+\mathrm{\Delta }t)-t}=\frac{d{B}_{sys}}{dt}$$

 

$$B_{CV}={\int }_{CV}^{}\rho bdV$$

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_{CV}(t+\mathrm{\Delta }t)-B_{CV}(t)}{\mathrm{\Delta }t}=\frac{d{B}_{CV}}{dt}=\frac{d}{dt}{\int }_{CV}^{}\rho bdV$$

 

 

$$B=bm$$

$$dB=bdm$$

 

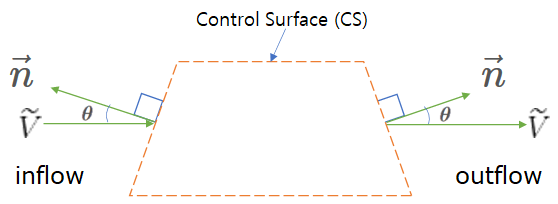
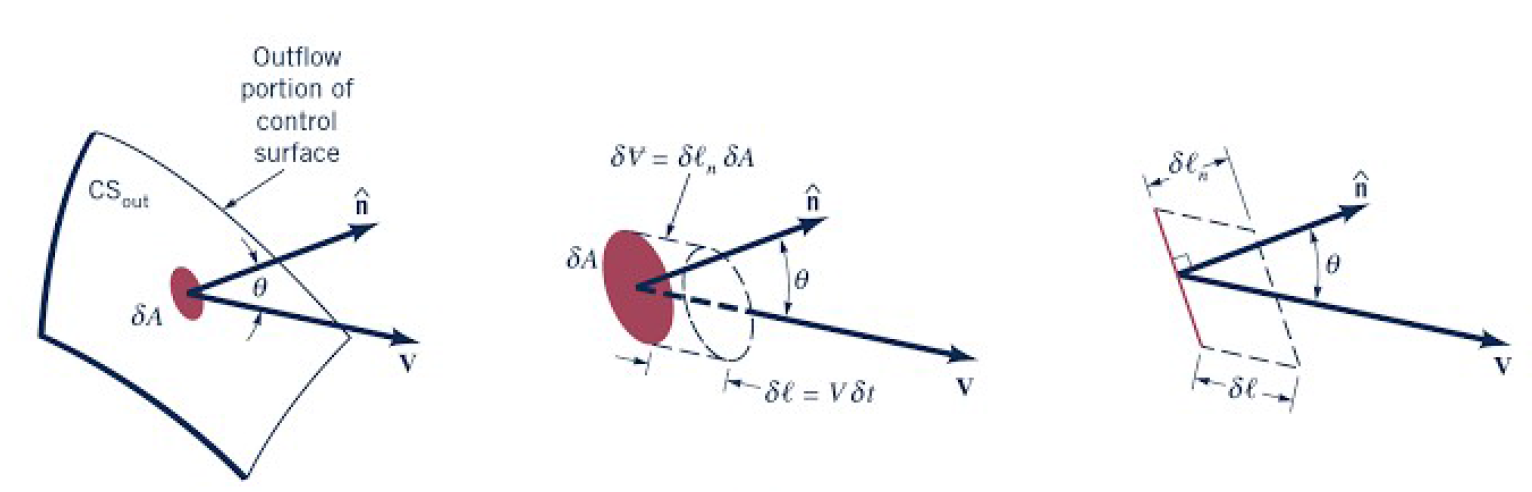
[2]

 

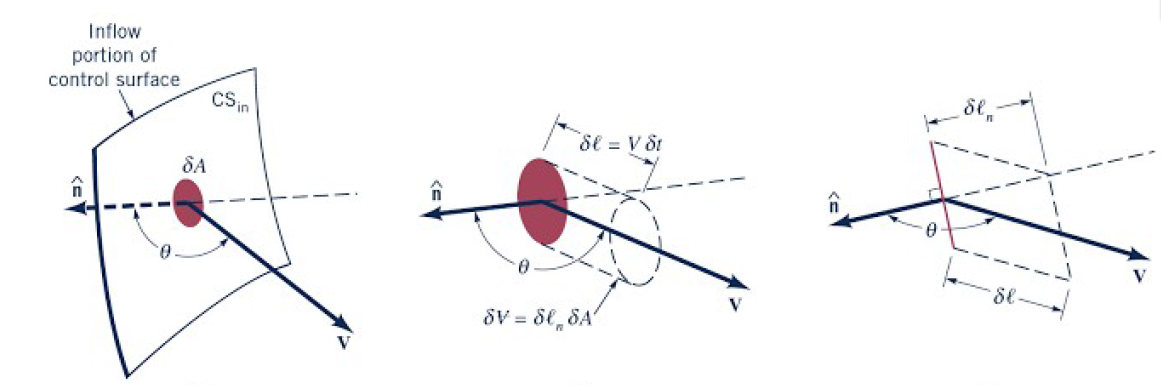
$$\theta <{90}^{\circ }(cos\theta >0)$$

 

$$d{m}_{out}=\rho dV$$

 

$$dV=(d{l}_n)(dA)$$

$$d{l}_n=(dl)(cos\theta )$$

$$dl=(\tilde{V})(\mathrm{\Delta }t)$$

$$dV=(\tilde{V})(\mathrm{\Delta }t)(cos\theta )(dA)$$

 

$$d{B}_{out}=bd{m}_{out}$$

$$d{B}_{out}=b\rho (\tilde{V})(\mathrm{\Delta }t)(cos\theta )(dA)$$

 

$${\int }_{C{S}_{out}}^{}d{B}_{out}=B_{II}(t+\mathrm{\Delta }t)$$

$${\int }_{C{S}_{out}}^{}d{B}_{out}={\int }_{C{S}_{out}}^{}b\rho (\tilde{V})(\mathrm{\Delta }t)(cos\theta )(dA)$$

 

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_{II}(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

$$\equiv {\dot{B}}_{out}$$

 

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_{II}(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

$$=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{1}{\mathrm{\Delta }t}({\int }_{C{S}_{out}}^{}b\rho (\tilde{V})(\mathrm{\Delta }t)(cos\theta )(dA))$$

$$={\int }_{C{S}_{out}}^{}b\rho (\tilde{V})(cos\theta )(dA)$$

 

$$\tilde{V}(cos\theta )=\overrightarrow{\tilde{V}}\cdot \overrightarrow{n}$$

 

$${\dot{B}}_{out}=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_{II}(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

$$={\int }_{C{S}_{out}}^{}b\rho \overrightarrow{\tilde{V}}\cdot \overrightarrow{n}(dA)$$

 

 

[2]

 

$$\theta >{90}^{\circ }(cos\theta <0)$$

 

$$d{m}_{in}=\rho dV$$

 

$$dV=(d{l}_n)(dA)$$

$$d{l}_n=(dl)(-cos\theta )$$

$$dl=(\tilde{V})(\mathrm{\Delta }t)$$

$$dV=(\tilde{V})(\mathrm{\Delta }t)(-cos\theta )(dA)$$

 

$$d{B}_{in}=bd{m}_{in}$$

$$d{B}_{in}=b\rho (\tilde{V})(\mathrm{\Delta }t)(-cos\theta )(dA)$$

 

$${\int }_{C{S}_{in}}^{}d{B}_{in}=B_I(t+\mathrm{\Delta }t)$$

$${\int }_{C{S}_{in}}^{}d{B}_{in}={\int }_{C{S}_{in}}^{}b\rho (\tilde{V})(\mathrm{\Delta }t)(-cos\theta )(dA)$$

 

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_I(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

$$\equiv {\dot{B}}_{in}$$

 

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_I(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

$$=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{1}{\mathrm{\Delta }t}({\int }_{C{S}_{in}}^{}b\rho (\tilde{V})(\mathrm{\Delta }t)(-cos\theta )(dA))$$

$$={\int }_{C{S}_{in}}^{}b\rho (\tilde{V})(-cos\theta )(dA)$$

 

$$\tilde{V}(cos\theta )=\overrightarrow{\tilde{V}}\cdot \overrightarrow{n}$$

 

$${\dot{B}}_{in}=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{B_I(t+\mathrm{\Delta }t)}{\mathrm{\Delta }t}$$

$$=-{\int }_{C{S}_{in}}^{}b\rho \overrightarrow{\tilde{V}}\cdot \overrightarrow{n}(dA)$$

 

 

$$\frac{d{B}_{sys}}{dt}=\frac{d{B}_{CV}}{dt}+{\dot{B}}_{out}-{\dot{B}}_{in}$$

$$\frac{d{B}_{sys}}{dt}=\frac{d}{dt}{\int }_{CV}^{}\rho bdV+{\int }_{C{S}_{out}}^{}b\rho \overrightarrow{\tilde{V}}\cdot \overrightarrow{n}(dA)-(-{\int }_{C{S}_{in}}^{}b\rho \overrightarrow{\tilde{V}}\cdot \overrightarrow{n}(dA))$$

$$\frac{d{B}_{sys}}{dt}=\frac{d}{dt}{\int }_{CV}^{}\rho bdV+{\int }_{CS}^{}b\rho \overrightarrow{\tilde{V}}\cdot \overrightarrow{n}(dA)$$

 

B=m 인 경우

질량보존법칙은 아래와 같다.

$$0=\frac{d{m}_{sys}}{dt}=\frac{d{m}_{CV}}{dt}+{\dot{m}}_{out}-{\dot{m}}_{in}$$

$$\frac{d{m}_{CV}}{dt}={\dot{m}}_{in}-{\dot{m}}_{out}$$

 

B=E 인 경우

에너지보존법칙(열역학 제1법칙)은 아래와 같다.

$$0=\frac{d{E}_{sys}}{dt}=\frac{d{E}_{CV}}{dt}+{\dot{E}}_{out}-{\dot{E}}_{in}$$

$$\frac{d{E}_{CV}}{dt}={\dot{E}}_{in}-{\dot{E}}_{out}$$

 

 

 

 

 

 

---

[1] Cengel, Yuns A.; Cimbala, John M. (2018). Flouid Dynamics: Fundamentals and Applications (4th ed.). McGraw-Hill. pp. 164-171.

[2] Gerhart, Philip M.; Gerhart, Andrew L.; Hochstein John I. (2018). Munson, Young, and Okiishi's Fundamentals of Fluid Mechanics (8th ed.). Wiley. pp. 175-187.